- 会員限定
- 2021/03/20 掲載
ウイルス検査を「ベイズ統計」で解説、なぜ闇雲なウイルス検査は誤判定が多くなる？
記事をお気に入りリストに登録することができます。
私たちが普段接する従来の統計学にはデータが必要です。データがなければ「議論できない」からです。ところがベイズ統計は、事前にデータがなくても、仮定しつつ議論を進め、情報を得ながら確率を更新していける強みがあります。ベイズ統計は、結果から原因、未来から過去を探るときにも活躍し、スパムメールの判定からビッグデータの分析まで、現在、幅広く応用されています。ここではウイルス検査を題材に、「なぜ闇雲なウイルス検査は誤判定が多くなるのか？」について、『いちばんやさしいベイズ統計入門』の著者がベイズ統計を用いてわかりやすく解説します。
1980年、宮城県仙台市生まれ。東京理科大学理学部第一部数学科卒業後、東北大学大学院理学研究科数学専攻修了。防衛省海上自衛隊数学教官。数学検定1級、算数・数学思考力検定（旧iML国際算数・数学思考力検定）1級、G検定（JDLADeep Learning For GENERAL 2020# 2）取得。大学在学時から早稲田アカデミーで指導経験を積む。担当した中学2年生の最下位クラスでは、できる問題から「やってみせ」、反復演習「させてみて」、「ほめて」伸ばす山本五十六式メソッドで、自信をつけさせることに成功。開成・早慶付属校に毎年合格している選抜クラスの平均を超える偉業を達成。その後、代々木ゼミナールの最年少講師を経て現職。海上自衛隊では、数学教官としてパイロット候補生に対する入口教育の充実、発展に大きく尽力した功績が認められ、事務官等（事務官、技官、教官）では異例の3級賞詞を受賞する。主な著書は『いちばんやさしいベイズ統計入門』（SBクリエイティブ）、『身近なアレを数学で説明してみる』（SBクリエイティブ）、『かけ算とわり算で面白いほどわかる微分積分』（ソーテック社）。『読売中高生新聞』のコーナー「リス（理数）る」も担当している。
例題1：6割正しい検査で感染しているかわかるか？
■例題1
P検査は、Cウイルスに感染している人に対して60％の確率で正しい判定「陽性」を下します。この検査で「Cウイルスに感染している」と判定されている人が、実際にCウイルスに感染している確率はいくらでしょうか？
P検査は、Cウイルスに感染している人に対して60％の確率で正しい判定「陽性」を下します。この検査で「Cウイルスに感染している」と判定されている人が、実際にCウイルスに感染している確率はいくらでしょうか？
「P検査は60％の確率で正しい判定「陽性」を下すから、Cウイルスに感染している確率は60％！」
……と答えるかもしれませんが、正解は「わからない」です。
なぜなら、Cウイルスに感染していない人の情報がないからです。「Cウイルスに感染している人に対して40％の確率で誤判定」となるので、Cウイルスに感染していない人を誤判定してしまう確率があるはずです。この「Cウイルスに感染していない人に対する判定確率」がないので、正確な確率が出せません。
このような検査では感度と特異度という概念を使うので、まずそれを解説します。
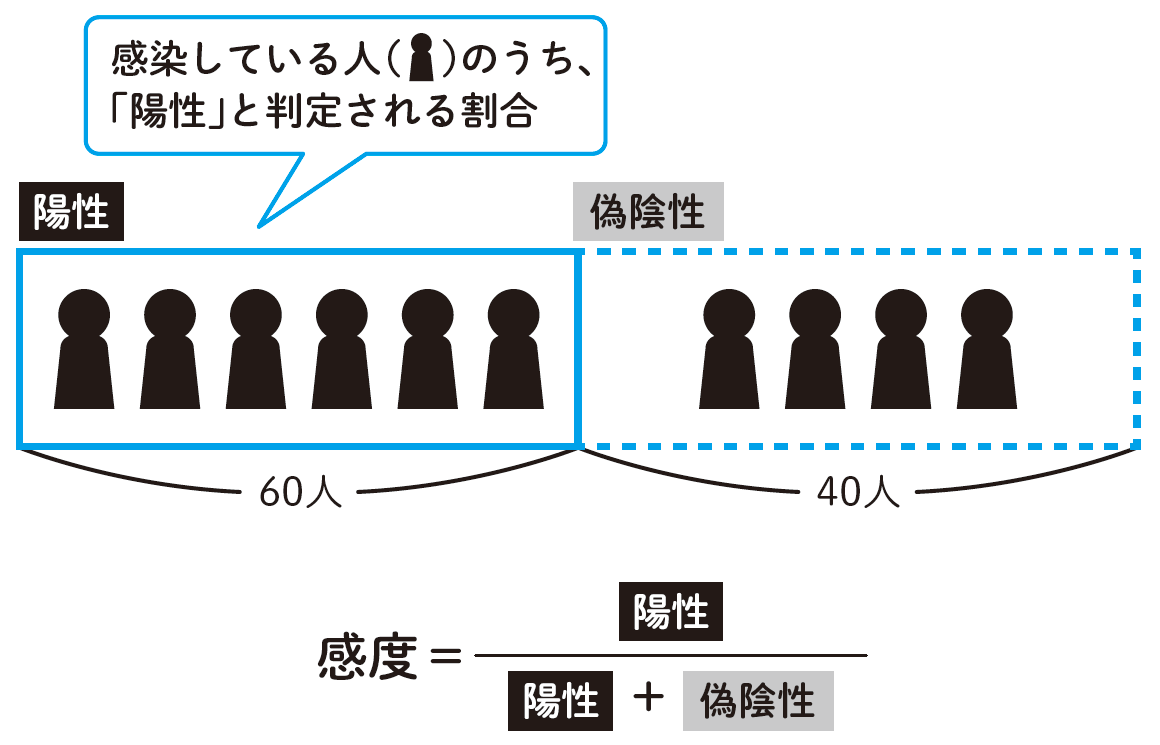
「感度」は「正しく陽性と判定される確率」
感度は、ウイルスに感染している人が、正しく陽性と判定される確率のことです。感度60％の場合、感染者100人のうち60人が正しく陽性と判定され、残りの40人が陰性と誤判定されます。誤判定された陰性を偽陰性といます。
「特異度」は「正しく陰性と判定される確率」
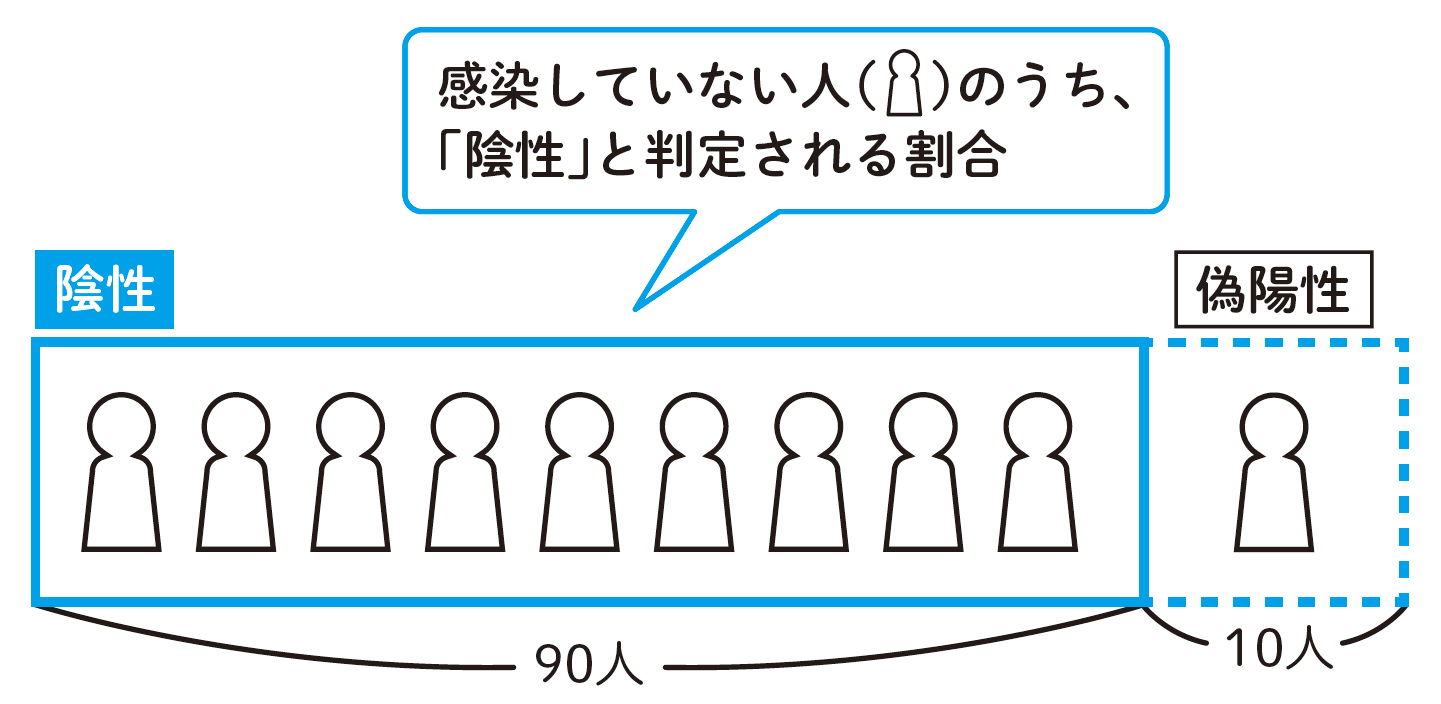
次に特異度は、ウイルスに感染していない人が、正しく陰性と判定される確率のことです。特異度90％の場合、感染者100人のうち90人が正しく陰性と判定され、残りの10人が陽性と誤判定されます。誤判定された陽性を偽陽性といいます。
私たちは「体の調子が悪いなあ……病気にかかっていないかな？ ウイルスに感染していないか？」と思い病院に行き、検査・診断してもらいます。医療では、病気やウイルス感染の判定方法が数多くありますが、100％判定できる検査法は、ほぼ存在しません。そこで、検査を受ける上で知っておきたい知識を、具体的な問題を通して知っておきましょう。
例題2：検査で「陽性」判断されたときに感染している確率は？
■例題2
Cウイルスに感染している人に対して、P検査は60％の確率で正しく陽性と判定します。また、Cウイルスに感染していない人に対して、P検査は90％の確率で正しく陰性と判定します。日本人でCウイルスに感染している人と感染していない人の割合は0.01％と99.99％とします。検診を受けた人がP検査で「陽性」と判断されたとき、その人が実際にCウイルスに感染している確率はどれくらいでしょうか？
Cウイルスに感染している人に対して、P検査は60％の確率で正しく陽性と判定します。また、Cウイルスに感染していない人に対して、P検査は90％の確率で正しく陰性と判定します。日本人でCウイルスに感染している人と感染していない人の割合は0.01％と99.99％とします。検診を受けた人がP検査で「陽性」と判断されたとき、その人が実際にCウイルスに感染している確率はどれくらいでしょうか？
問題文から、Cウイルスに感染している人が、P検査で正しく判定される確率（感度）は60％なので、間違った判定をされる確率は100－60＝40（％）です。Cウイルスに感染していない人が、P検査で正しく判定される確率は90％なので、間違った判定をされる確率は100－90＝10（％）です。
この状況を表にまとめてみます。
この例題では、P検査で「陽性」と判断された人が、実際にCウイルスに感染している確率を求めたいので、太枠の部分に着目してみましょう。
確率の問題は、どうしても分数が必要になります。分数式を見ると苦手意識が出てくる人がいると思うので、ここでは、具体的な数に置き換えてみましょう。たとえば、今回の問いを「100000（10万）人」に適用してみます。
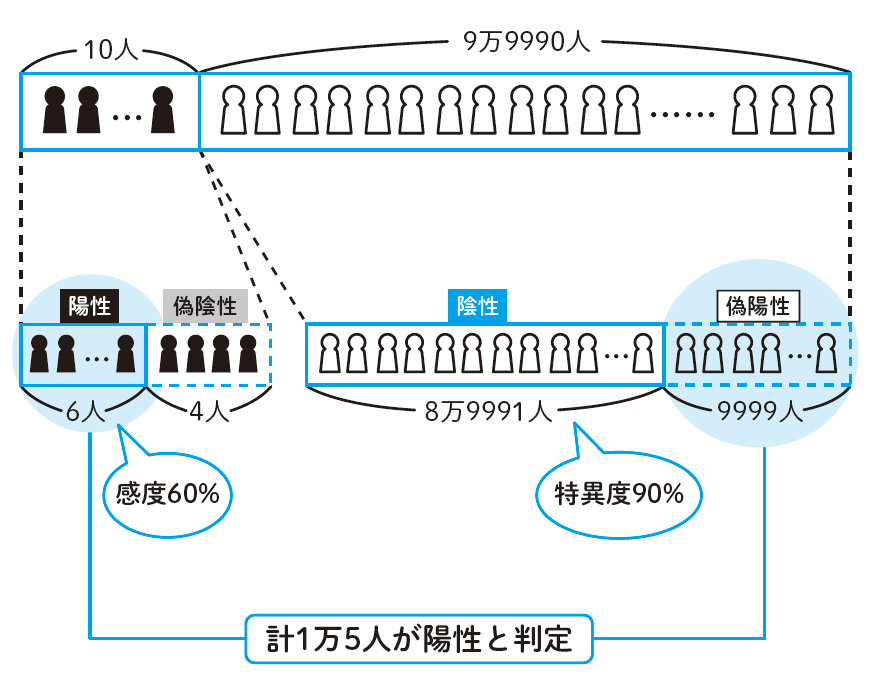
Cウイルスに感染しているのは0.01％なので、
100000×0.0001＝10（人）
Cウイルスに感染していないのは、100000－10＝99990（人） です。
Cウイルスに感染している10人中、陽性は60％なので、
10×0.6＝6人
Cウイルスに感染している10人中、陰性は40％なので、
10×0.4＝4人
Cウイルスに感染していない99990人中、陽性は10％なので、
99990×0.1＝9999（人）
Cウイルスに感染していない99990人中、陰性は90％なので、
99990×0.9＝89991（人）です。
これを表にまとめると以下のようになります。
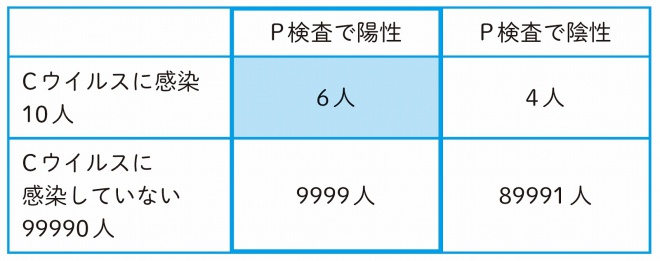
【次ページ】とんでもない数の誤判定が出てしまうワケ
関連タグ
あなたの投稿
PR
PR
PR
