ついつい買ってしまった缶コーヒー

　私は今まで、あまり缶コーヒーを飲んだことがなかった。

　でも、「ジョージア」のテレビCMは不思議と印象的で、ずっと気になっていた。今まで缶コーヒーのCMが目に留まったことなどなかったのに、この商品だけは何か違った。そしてある平日のお昼、コンビニでサンドイッチを買ったときに、「あ、これだ」と、つい「ジョージア」をカゴに入れてしまったのだ。

　そこで、ふと疑問に思った。ふだん缶コーヒーを買わない私が、CMに惹ひかれて、つい買ってしまった。自分を振り返ってみると、「糖分ゼロ」「本格的な味わい」といった、いわゆるスペック的な面もさることながら、CMの雰囲気やストーリー性に好感を抱いたのだ。

　では、世の中の人たちは、いったいどうやって缶コーヒーを選んでいるのか。私と同様、やはりCMにどれくらい好感を抱くかがカギとなっているのだろうか？

買ったのは「たまたま」か？　「CMがおもしろかったから」か？

　CMに好感を抱くと、缶コーヒーの売上は伸びるのか。この問題では、統計学の「相関」という考え方が使える。相関とは、「1つの事柄が、別の事柄の変化に影響している」ということ。これには3つのタイプがある。

　1つ目は、「正の相関」。ある1つの事柄が大きくなると、別の事柄も大きくなるという相関だ。要するに、「同じ方向に動く」ということだ。

　たとえば、「身長と体重」などは正の相関の代表格だ。確かに、身長が高くなれば、体重は重くなる傾向がある。また、近年は変化しつつあるとはいわれているが、「学歴と年収」にも、いまだに正の相関が見られる。ほかには、どんな「正の相関」があるだろう？

　そうだ、暑くなればなるほど飲みたくなるもの……「気温とビール消費量」なども正の相関になるはずだ。それをいうなら、もちろん「気温とかき氷消費数」とか「気温とアイスクリーム消費数」も同様だ。寒くても冷たいものを食べたり飲んだりする人はいるが、総じて、気温が高くなるほどに冷たいものがほしくなる。挙げだしたらキリがないから、ここらでやめておこう。

　2つ目は、「負の相関」。1つ目の「正の相関」とは逆に、ある1つの事柄が大きくなると、別の事柄は小さくなるという相関だ。正の相関は「同じ方向に動く」が、負の相関だと「逆の方向に動く」ということだ。


　負の相関は、どんな事柄に見られるか。たとえば、一定の年齢以上は年を重ねるにつれて体力が落ちるから、「一定年齢以上の年齢と体力」は、負の相関になるだろう。また、月収20万円の人は、月の消費額が高いほどに貯蓄額は低くなる。「月収20万円に対する消費と貯蓄の相関」も、負の相関になるわけだ。さっきのような気温でいえば、「気温とおでん消費量」は、ビールやかき氷とは逆に「負の相関」になる。

　そして3つ目は、正の相関でも負の相関でもない「無相関」だ。

　たとえば、「身長とベルト保有数」は、どうだろう。身長が高い人ほど多くのベルトを持っているなんて聞いたことがないし、逆に身長が高いほどに、持っているベルトの本数が減る、なんて話も聞いたことがない。ちょっと荒唐無稽な例だったかもしれないが、ともあれ、1つの事柄が、別の事柄の変化に影響していないというのが、無相関だ。

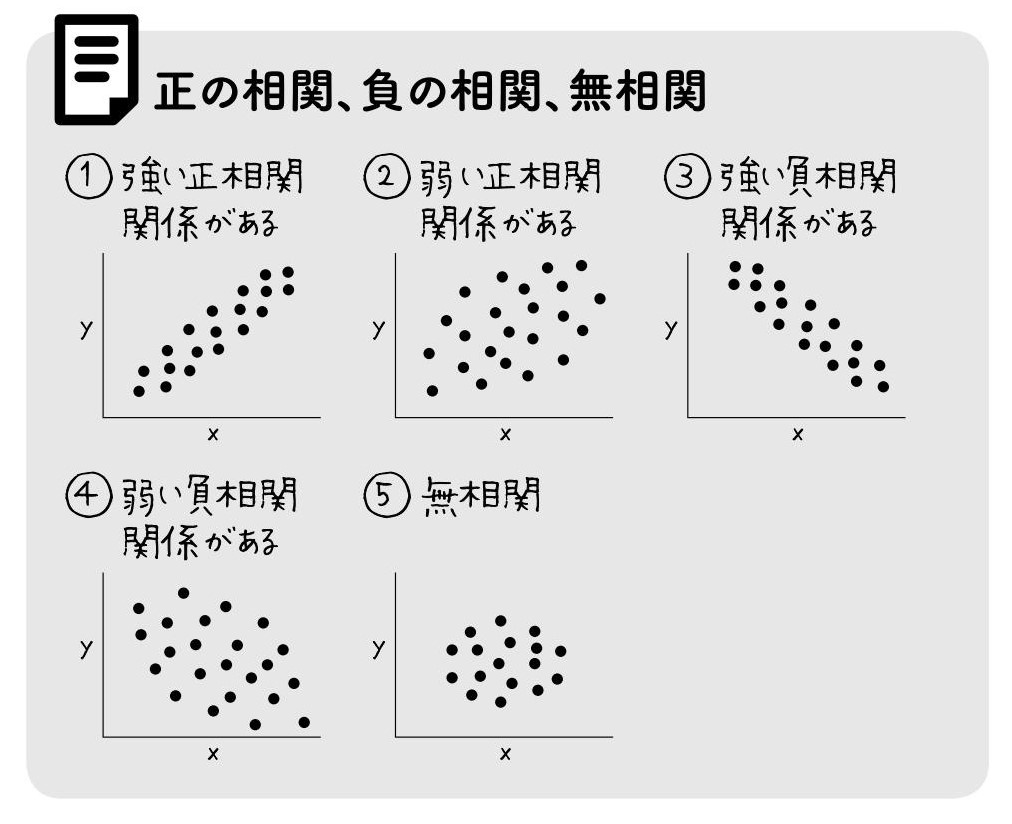
　正の相関、負の相関、無相関は、おおよそ下のような図になる。この縦軸（y軸）と横軸（x軸）には、きっと見覚えがあると思う。そう、中学校で習う「関数のグラフ」だ。xがいくつのとき、yはいくつになる……というやつだ。それを統計学では「散布図」と呼ぶのである。


　これらの点の1つひとつが、観測されたデータだ。1つの事柄と別の事柄という2つのデータが得られるとき、一方をx、もう一方をyとして、座標（x、y）のところに点を打つ。ただし、点がきれいに一直線に並ぶとは限らない。というより、現実世界では図のようにまばらになるのが当たり前だ。

　たとえば、いくら身長と体重は正の相関といっても、身長150㎝の人全員が45㎏、身長160㎝の人全員が50㎏……と決まっているはずがない。つまり、観測されたデータはさまざまだから、ある程度、散らばることになり、まさに「散布図」という名のとおりの見た目となるわけだ。

　この散布図上の点を囲んだときに、右上がりのサツマイモのような形になったら正の相関、右下がりのサツマイモのような形になったら負の相関だ。無相関の場合は、あらゆるところに点が打たれるところになるから、おおよそ丸型になる。

「サツマイモ」の向きと太さは？

　相関については、これでだいたいわかってもらえただろう。

　次に話したいのは、相関係数の「係数」とは何か、である。といっても概念的な説明はひと言で済む。係数とは、簡単にいえば「2つの事柄は、おおよそ、どの程度、関係しているのか？」だ。

　たとえば兄弟と姉妹の身長のデータを、さっきのような散布図にすると、けっこう点が散らばる。それでも、傾向としては、ゆるやかに右上がりになることから、「兄弟の身長が高ければ、“必ず”姉妹の身長も高い」とはいえないまでも、「兄弟の身長が高ければ、“おおよそ”姉妹の身長も高い傾向にある」とはいえる。係数とは、この“おおよそ”の程度を数値で評価する、ということなのだ。

　ここで先ほどの散布図を、もう一度、見てほしい。

　右上がりのサツマイモも右下がりのサツマイモもあるが、太さがいろいろだろう。データの点の散らばり具合が、より狭い（線に近い）散布図は、相関がより強い。つまり、「より細いサツマイモ」ほど、xとyという2つの事柄の相関性は「より強い」ということだ。

　このように、相関係数とは「2つの事柄は、おおよそ、どの程度、関係しているか？」だと覚えておけばいい。サツマイモの形はどうか、向きはどうなっているか、どれくらい太っているのかを指標化するということだ。

【次ページ】CMとコーヒーの売上の関係を探るには、「相関係数」を使う